Negative binomial distribution

This function determines the probability that there will be F failures before the Nth success (S) with a constant probability of success P. The negative binomial distribution is similar to the binomial distribution, but the number of successes is fixed and the number of trials is variable.

As in the binomial distribution, trials are assumed to be independent. For example, to find ten individuals with excellent reflexes, knowing that the probability that a candidate has these qualifications is 0.3, this function calculates the probability that a certain number of unqualified candidates will be interviewed before the ten people sought are selected.

Syntax

NegativeBinomialDistribution(F, S, P)

Where:

F is the number of failures.

S is the threshold number of successes.

P is the probability of a success.

Expression

In the expression that follows, F = x, S = r.

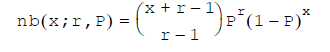
Usage Notes

If either F or S is not an integer, it is truncated.

The following conditions are invalid:

• One of the arguments is nonnumeric.
• P< 0 or P> 1.
• F + (S - 1) £ 0.